统计学下的假设检验

奋斗吧

擅长邻域：未填写

2023-05-10 18:23:24 60浏览

由于本人才疏学浅，再加上时间仓促，难免有疏漏之处，恳请批评指正.1,预备知识数理统计：以概率论为基础，研究如何有效的去搜集、整理、分析带随机性影响的数据总体与样本：研究对象的全体就称为总体样本：假设需要测试某一个指标X，从总体中抽取n个个体，且这n个个体的指标为（）,则称这n个个体的指标为一个样本统计量：样本来自于总体，是总体的反映，是进行总体的推断的依据。然而，分散的样本统计意义不明显，需要对样本进行浓缩，

由于本人才疏学浅，再加上时间仓促，难免有疏漏之处，恳请批评指正.

1,预备知识

数理统计：以概率论为基础，研究如何有效的去搜集、整理、分析带随机性影响的数据

总体与样本：研究对象的全体就称为总体

样本：假设需要测试某一个指标X，从总体中抽取n个个体，且这n个个体的指标为（ $X_1,X_2,X_3,......,X_n$ ）,则称这n个个体的指标为一个样本

统计量：样本来自于总体，是总体的反映，是进行总体的推断的依据。然而，分散的样本统计意义不明显，需要对样本进行浓缩，构造一个合适的依赖样本的函数来解决问题，这种函数就称为统计量

常见的统计量包括：样本均值，样本方差，样本标准差，样本k阶原点矩，k阶中心矩。

抽样分布：统计量的分布即抽样分布。统计量是样本的函数，抽样分布函数可以从样本的联合分布函数中推出，当总体的分布函数已知，则抽样分布也是确定的。这里大家先主要了解抽样分布有哪些，抽样分布对于假设检验，构造统计量有很大的帮助。

下面简单介绍有哪些抽样分布及其简单的构造形式，具体的性质不做赘述，大家自行查阅。

1） $\chi ^2$ 分布：设 $X_1,X_2,X_3,......,X_n$ 独立同分布与 $N(0,1)$ 标准正态分布，则称统计量

$\chi^2 = X_1^2 + X_2^2 + ...... + X_n^2$

服从自由度为 n的 $\chi ^2$ 分布，记为 $\chi ^2$ ~ $\chi ^2(n)$

2）F分布：设U ~ $\chi^2(m)$ ， V ~ $\chi ^2(n)$ ,且U，V相互独立，则称随机变量

$F = \frac{\frac{U}{m}}{\frac{V}{n}}$

服从自由度为(m ,n)的F分布，记为F ~ F(m, n)

3) t分布：设X ~ $N(0, 1)$ ，Y ~ $\chi ^2(n)$ ,且X和Y独立，则称随机变量

$t = \frac{X}{\sqrt{Y/n}}$

服从自由度为n的t分布，记为t ~ t(n).

2,统计学中的假设检验

2.1 导论

统计推断是利用样本资料中的所得到的信息估计有关总体的一些未知参数。而假设检验问题，也差不多，是利用已经采样的信息去对未知的参数进行估计。

举一个简单的例子，某公司过去很长一段时间的不合格率不超过0.01，某天随机抽样100件，发现有3件产品不合格，那不合格的产品出现的频率是0.03。显然，当天的不合格率已经超过了0.01，这能说明生产过程已经不稳定了吗？

其实不然，这个时候就需要用更加具体的数学方法进行检验，这一类问题就是假设检验问题。

再仔细分析一下上面的问题，当天所以进行抽样一次的产品其实满足于一个二项分布B(1, $\theta$ )(0< $\theta$ <1)，这里的 $\theta$ 是产品的不合格率，于是所谓的生产过程就是 $\theta \leqslant 0.01$ ，否则就是 $\theta > 0.01$

，于是就将原始的问题转化为统计假设问题。

针对上面问题，提出两个猜想：原假设 $H_0$ 和备择假设 $H_1$ ，数学语言表示为：

$H_0:\theta \leq 0.01\leftrightarrow H_1 > 0.01$

这里就涉及到原假设和备择假设的理解：一般来说，我们定义原假设和备择假设是一对互补的命题。原假设和备择假设我认为有一个用途，就是便于转化为统计的问题求解概率。

通过一些操作，判断在当前的采集的样本下，满足原假设的概率，如果概率很小，就认为这是一个小概率事件，几乎不可能发生，那么就拒绝原假设（认为原假设是错误的），否则就接受原假设。

以上就是假设检验最根本的思想，再换一种更加便于理解的来阐述：在一定的统计假设的前提下，如果发生了小概率事件，就有理由怀疑假设的真实性，从而拒绝原假设。小概率事件不会发生。

现在已经对假设检验的思想有了基本的了解，了解了什么是原假设和备择假设。

2.2 检验统计量，临界值和拒绝域

前面讲到了，对原始问题需要经过一系列操作，将其转化为概率问题，并判断这是否是一个小概率事件。现在就讲解这个操作是什么。

现在我们已经采集了一些样本，但是还需要对样本进行加工，把样本中的关于总体未知参数的信息集中起来，构造一个适合于检验假设的统计量 $T = T(\tilde{X})$ ，一般来说，假设检验最难的部分就是构造合适的检验统计量。

在本题中，可以设置 $T = T(\sum_{i = 0}^{100} X_i)$ ，则T服从二项分布 $B(100, \theta)$ , 明显的，当T处在一个较小值， $H_0$ 为真；否则 $H_0$ 不真。因此，我们可以提前设置一个阈值C,则有

$\sum_{i=1}^{100}x_i \geq C$ ,拒绝原假设

$\sum_{i=1}^{100}x_i < C$ , 接受原假设

这里的T就称为检验统计量（就是这个玩意最难搞）和阈值。

拒绝域就是处于可以拒绝原假设的样本空间范围内的样本，转化为数学语言就是：

$W = \{\tilde{x} = (x_1, x_2, x_3,...,x_{100}) | \sum_{i=1}^{100}x_i \geq C\}$

$\bar{W} = x - W$

当样本的观察值属于W的时候，就拒绝原假设，就称为拒绝域。还有接受域。

2.3 两类错误

第一类错误：原假设本身是正确的的（本题中，这个生产过程本就不稳定，观察值却显示的异常，落到了拒绝域中），但是做出了 $H_0$ 不真的判断，犯了“弃真”的错误。

第二类错误：原假设是错误的，但是判断成正确的，犯了“存伪”的错误。

通常来说，这两类错误是互斥的，要较小第一类错误，减小 $\alpha(\theta)$ (在参数为theta的情况下，犯第一类错误的概率)，就需要扩大临界值C，减小拒绝域。而要减小第二类错误，就需要减小临界值C的范围，增大拒绝域。

于是，大佬奈曼（Neyman）和皮尔逊（Pearson）就说，要先控制第一类的错误（不能冤枉一个好人），给定一个 $\alpha$ (显著性水平 )，限制第一类错误不超过 $\alpha$ ，在此基础上，再尽可能的减小第二类错误。这就是假设检验中著名的N - P准则。

2.4 水平为 $\alpha$ 的检验（相当于对前面的解答）

犯第一类错误的概率不超过 $\alpha$ 的检验称为显著性水平为 $\alpha$ 的检验，简称为水平为 $\alpha$ 的检验。

则这里的拒绝域是：

$W = \{\tilde{x} = (x_1, x_2,......,x_{100}) | \sum_{i=1}^{100}x_i \geq C, x_i=0,1 (i = 1, 2, 3,......, 100)\}$

那么，在本题中的犯第一类错误的概率就是：

$\alpha(\theta) = P(\bar{X} > C | \theta \leq \theta_0) = \sum_{j = C+1}^{100}\binom{100}{j}\theta^j(1-\theta)^{100-j}$

根据二项分布的p检验，可知 $max(\alpha(p)) = \alpha(p_0) = \alpha(0.01)$ ,则

$\alpha(0.01) = \sum_{j = C+1}^{100}\binom{100}{j}\0.01^j(0.99)^{100-j} \leq \alpha$

此时需要再 $C \in [C^*,+\infty ]$ ,找到一个最小值 $C^*$ 。最后重要的一步，写出拒绝域，便于后续进行判断：

$W = \{\tilde{x} = (x_1, x_2,......,x_{100}) | \sum_{i=1}^{100}x_i \geq C^*, x_i=0,1 (i = 1, 2, 3,......, 100)\}$

若100件抽样产品中，发现了3件不合格品。

在 $\alpha$ = 0.1时， $C^*$ = 3，此时 $\sum_{i=1}^{100}x_i \geq C^*$ ,则落在拒绝域中，拒绝H0，认为生产过程不稳定。从置信水平来看，现在有90%的把握认为可以拒绝H0，认为生产过程不稳定。

在 $\alpha$ = 0.05的时候， $C^*$ = 4，此时 $\sum_{i=1}^{100}x_i \geq C^*$ ,则落在拒绝域中，不能拒绝H0，认为生产过程稳定正常。从置信水平上来看，有95%的把握，可以拒绝H0，认为生产过程认为生产过程不稳定。但是这样的程度就降低了。

这里面的细节可以好好体味一下。

2.5 一般处理假设检验的步骤

根据实际问题，提出原假设 $H_0$ 和备择假设 $H_1$
确定检验统计量T(x)
确定第一类错误 $\alpha$ 的表达形式，记住需要利用统计量进行表达，这样便于求出阈值
设置显著性水平 $\alpha$ ,并使得犯第一类错误的概率最大值尽可能的接近 $\alpha$ ，求出统计量的阈值，并写出其拒绝域的表达形式
最后，计算统计样本的检验统计量的值，并判断其是否落在拒绝域中，若落入拒绝域，则拒绝H0

下面开始介绍一些常见的假设检验的方法，都是基于正态分布衍生出来的分布，其中包括常见的t检验，F检验等等，会逐一的系统性的介绍到

2.6 单个正态总体的假设检验

前提：认定 $X_1,X_2,......,X_n$ 均来自于正态总体 $N(\mu, \sigma^2)$ 的样本，记为：

$\bar{X} = \frac{1}{n}\sum_{i = 1}^{n}X_i$ , $S^2 = \frac{1}{n-1}\sum_{i=1}^{n}(X_i - \bar{X})^2$

2.6.1 单个正态分布总体均值的假设检验

1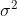， $\sigma^2$ 已知

（1） $H_0:\mu\geq\mu_0\leftrightarrow H_1:\mu<\mu_0$

这种情况，就先完整的按照之前的步骤进行写一遍。

1）原假设和备择假设已给出
2）确定检验统计量，这里需要对 $\mu$ 进行检验，我们可以选择 $\bar{X}$ 作为检验统计量

3）确定拒绝域：由于 $\bar{X}$ 是 $\mu$ 的估计，因此，当H0为真的时候， $\bar{X}$ 不应该太小，于是给出拒绝域

$W = \{(x_1,x_2,...,x_n)|\bar{x}\leq C\}$

4)确定发生第一类错误的概率：

$\alpha(\mu) = P\{\bar{X} \leq C | \mu \geq \mu_0 \} = \phi(\frac{C-\mu}{\sigma/\sqrt{n}})$

由于其是正态分布，故可以转化为标准正态分布的概率累计函数。其中 $\mu \in (\mu_0, +\infty)$ ,在 $\mu = \mu_0$ 取得最大值

$max_{\mu \geq\mu_0}\alpha(\mu) = \phi(\frac{C - \mu_0}{\theta/\sqrt n}) = \alpha$

$\frac{C - \mu_0}{\theta/\sqrt n} = z_{1-\alpha}$

这一步的转化，首先需要理解什么是上分位点 $z_\alpha$ ,就是在置信水平为 $1 - \alpha$ 下，从 $[-\infty,z_\alpha]$ 其概率的累计值为 $1-\alpha$ 的值。但是在这里的 $\alpha$ 是显著性水平。因此，需要转化为 $z_{1-\alpha}$ .

举一个例子，假设现在取显著性水平 $\alpha$ = 0.05,则

$z_{1-\alpha} = z_{0.95} = -1.645$ ,

意思是当取值为-1.645时，这里定义的是上分位 $\alpha$ 点的值，则>-1.645概率有95%。若U小于-1.645,则认为其是小概率事件，应当拒绝原假设。

（2） $H_0:\mu\leq\mu_0\leftrightarrow H_1:\mu>\mu_0$

同理可得，通过计算，这里的拒绝域可以设置为 $W = \{U \geq z_{\alpha}\}$ .

(3) $H_0:\mu =\mu_0\leftrightarrow H_1:\mu \neq \mu_0$

则这里需要进行双边假设，拒绝域应为 $W = \{ \bar{X}\left | U \right |\geq z_{\alpha/2} \}$

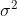2, $\sigma^2$ 未知

这个时候，前一节的统计量 $U = \frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}$ 就不满足，因为 $\sigma$ 未知,那么就用S来代替 $\sigma$ ，可以得到：

$U = \frac{\bar{X}-\mu_0}{S/\sqrt{n}} \sim t(n-1)$

具体推到的方法，类似于构造t分布得到的，这里不做详细的介绍。

这就是著名的t分布，在未知数据的方差的情况下，分布的均值做估计。在t分布中，X（参照上文中提到的公式）是服从标准正态分布的，于是要求t检验的数据也是要来自于正态分布。这个要求就比较苛刻了，也有说法说，只要数据量够大也可以直接使用t检验，因为有大数定理。详情可以参看博客不满足正态分布，到底能不能用t检验。这里先给出建议：

1，若原数据服从正态分布，则进行t检验

2，若原数据偏离正态分布较大，则进行非参数检验Wilcoxon rank-sum检验

3，若数据量较大：二者均可

若偏离程度较小，一般30个以上就可以执行t检验

若偏离程度较大，100个以上可以执行t检验